Rumus / Dasar Teori Impedansi

ANAMS.ID – Kali ini kita akan membahas terkait “Rumus / Dasar Teori Impedansi”
Artikel ini bertujuan untuk memberikan informasi terkait “Rumus / Dasar Teori Impedansi” agar supaya bermanfaat bagi pembaca
Simak artikel “Rumus / Dasar Teori Impedansi” dengan baik untuk mendapatkan keseluruhan insightnya.

Rumus / Dasar Teori Impedansi

persamaan:

Vs (t) = i(t) R + 1/C∫ i(t) dt
Dengan Vs(t) = Vp cos (Wt + ɸos) dan i(t) = Ip cos (Wt + ɸoi)
Dapat kita fikirkanVs(t) = Vp cos (Wt + ɸos)sebagai bagian nyata dari pada
(V_s ) ̅(t) = Vp ej(Wt + ɸos)
I(t) = Ip cos (Wt + ɸoi)sebagai bagian nyata daripada
i ̅(t) = Ip ej (Wt + ɸos)

selanjutnya(V_s ) ̅(t)= Vpe j(Wt + ɸos)……………………….. …. .(1.1)
dapat dituliskan sebagai
(V_s ) ̅ (t) = Vp ejØ os ej w t=(V_p ) ̅ e j w t……………………… …. . . . . . (1.2)
Dengan (V_p ) ̅= Vp ej ɸos kita sebut amplitudo kompleks

Karena kapasitansi kompleks memiliki dua kuantitas, yaitu perhitungan sudut fase konstan, dapat dianggap cepat. Jadi amplitudo kompleks adalah cara mengekspresikan fase menggunakan variabel kompleks.

Demikian pula, (t) = Ip e j (Wt + oi) = Ip e jɸoiejwt = ej w twith = Ip e jɸoiamplitudo kompleks untuk kompleks arus sesaat i (t), maka persamaannya. Kami menulis untuk (t) dan (t), sehingga kami mendapatkan;

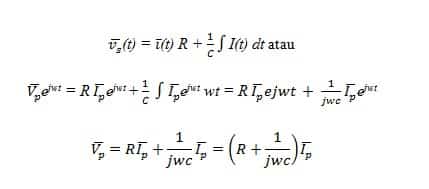
Arus bolak-balik

(V_p) = Z (I_p) ……………………………………………….. (1.3)
Dengan Z = R + 1 / jwC ……………………………………..(1.4)

Persamaan (1.3) menyatakan hubungan antara dan apa yang tampak seperti ohm, menggunakan besaran kompleks. Persamaan (1.3) memberikan hubungan antara fase, yang berarti bahwa itu mencakup besaran dan sudut fase. Besaran Z disebut impedansi kompleks, dan menggantikan peran resistansi R dalam rangkaian alternatif.

Dari persamaan (1.3) dan (1.4) diperoleh:

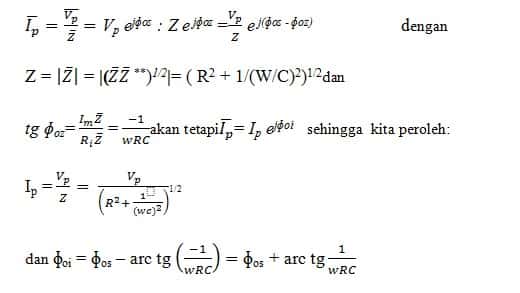
Hasilnya sama dengan yang kita dapatkan dengan menggunakan metode tasor. Keuntungan dari penyelesaian fungsi eksponensial kompleks dan impedansi kompleks adalah bahwa matematika dapat digunakan untuk menyatakan fase dan aturan arus searah dapat diterapkan selama jumlah tegangan, arus, dan resistansi yang kompleks digunakan.

Kapasitansi C bertindak sebagai resistansi:

(Z_C) = i / jWC = (- j) / WC = -jXc

Besaran Xc disebut reaktansi kapasitif. Berdasarkan alasan yang sama seperti di atas, induktansi L akan menyebabkan resistensi.

(Z_L) = jwL = jX_L

Kuantitas Xc disebut reaktansi induktif, dan pada frekuensi tinggi kapasitor memiliki reaktansi kecil. Sebaliknya, pada frekuensi yang lebih rendah, reaktansinya kecil. Di sisi lain, pada frekuensi yang lebih rendah memiliki reaktansi yang besar. Hal ini berbeda dengan induktansi L yang memiliki reaktansi besar pada frekuensi tinggi dan reaktansi kecil pada frekuensi rendah.

Baca Juga : Dua buah satelit A dan B mengorbit sebuah planet yang sama

Itulah pembahasan terkait artikel Rumus / Dasar Teori Impedansi. semoga bermanfaat***

anams.id Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya

Rumus / Dasar Teori Impedansi

Rumus / Dasar Teori Impedansi

Baca Juga Artikel Lainnya: